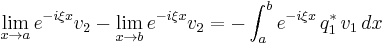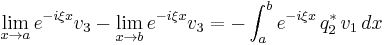Manakov system
Maxwell's Equations, when converted to cylindrical coordinates, and with the boundary conditions for an optical fiber while including birefringence as an effect taken into account, will yield the coupled nonlinear Schrödinger equations. After employing the Inverse scattering transform (a procedure analogous to the Fourier Transform and Laplace Transform) on the resulting equations, the Manakov system is then obtained. The most general form of the Manakov system is as follows:
It is a coupled system of linear ordinary differential equations. The functions 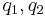 represent the envelope of the electromagnetic field as an initial condition.
represent the envelope of the electromagnetic field as an initial condition.
For theoretical purposes, the integral equation version is often very useful. It is as follows:
One may make further substitutions and simplifications, depending on the limits used and the assumptions about boundary or initial conditions. One important concept is that 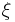 is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change sign; accordingly, most researchers take the imaginary part to be positive.
is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change sign; accordingly, most researchers take the imaginary part to be positive.
References
- C. Menyuk, Application of multiple-length-scale methods to the study of optical fiber transmission, Journal of Engineering Mathematics 36: 113-136, 1999, Kluwer Academic Publishers, Netherlands.
- D. Kaup, B. Malomed, Soliton Trapping and Daughter Waves in the Manakov Model, Physical Review A, Vol. 48, No. 1, July 1993.
- S. V. Manakov, Remarks on the Integrals of the Euler Equations of the n-dimensional Heavy Top, Functional Anal. Appl., Vol. 10, pp. 93–94, 1976.
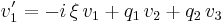
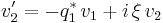
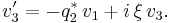
![\lim_{x\to a}e^{i\xi x}v_{1}-\lim_{x\to b}e^{i\xi x}v_{1}=\int_{a}^{b}[e^{i\xi x}\,q_{1}\,v_{2}%2Be^{i\xi x}\,q_{2}\,v_{3}]\,dx](/2012-wikipedia_en_all_nopic_01_2012/I/de7fde77a9631b05cd585341f53faa4f.png)